Q1 ⇒問題
不等号の概念、及び、数式の加減について触れておくことに狙いをおいた出題です。
まず、B3個よりもD2個が高値なので、B<D(価格を不等号で表すことにします)
次に、D3個よりもA2個が高値なので、D<A
そしてA+D=2×Cとあるので、上記とあわせ、
A、C、Dの関係が 小+大=中×2 が直感的にわかるかどうか。
ここがPOINTのひとつです。
以上を考え合わせると、B<D<C<A が導かれます。
次に、ABC、ABD、ACD、BCDの4つの組み合わせについて、
先ほど判明したB<D<C<Aより、
BDCが一番小さく、DCAが一番大きいことは一目瞭然なのですが、
BDC<BDA<BCA<DCAが見抜けることも重要。
上記不等号の隣同士の関係性において、残りふたつが一緒なのだから…
と自分で発見できればOK。
もしくは、Aが一番高価なのだから、Aが抜けている組み合わせが一番安いな…
と考えてもOK。B<D<C<Aの関係性からA抜け<C抜け<D抜け<B抜けとなります。
以上より、
BDC=76ソーラ
BDA=83ソーラ
BCA=90ソーラ
DCA=99ソーラ
となります。ここからは一番下の式DCA=99と、A+D=2×Cより、代入して、
Cが3つで99ソーラなので…と解く方法もあるのですが、
ここは式の加減で解説しておきます。
縦書きにそろえて書いてみるのがPOINTです。
B+D+C+A=76
B+D+C+A=83
B+D+C+A=90
B+D+C+A=99
4式ともB+D+C+Aからどれかひとつが抜け落ちた式ですから、
イコールの左側(左辺、といいます)を全て足すと、それぞれ鉱石が3つずつになります。
また、イコールの右側(右辺、といいます)は、76+83+90+99=348
整理すると、
(B+D+C+A)×3=348
となるので、ここから
B+D+C+A=116が求まります。
あとは
B+D+C+A=76
なので、A=116-76=40
B+D+C+A=83
なので、C=116-83=33
B+D+C+A=90
なので、D=116-90=26
B+D+C+A=99
なので、B=116-99=17
とすればクリアです!
A=40ソーラ、B=17ソーラ、C=33ソーラ、D=26ソーラ
Q2 ⇒問題
こよみ算、特にうるう年の扱いに触れることに狙いをおいた出題です。
まず、問題文のうるう年が何年になるのかは、暗記事項となりますので覚えましょう!
さて、うるう年でない一年(平年といいます)は365日です。
2015年1月1日は、実は2014年1月366日とみなしてもよいのです。
この発想は、こよみ算ではとても大事です。
一週間は7日ですから、7で割った余りが同じ数字の日は、同じ曜日になります。
2014年1月1日が水曜日なのだとしたら…
1÷7=0余り1なので、余り1が水曜日です。
2015年1月1日は、2014年1月366日とみなしてもよいので、
366÷7=52余り2なので、水曜日の次の木曜日になります。
ここでPOINT。
うるう年でない場合、ちょうど一年後の同じ日は、曜日が一日分進みます。
うるう年は2月29日の分ズレるので、つまりは曜日が二日分進みます。
あとは計算でもよいのですが、たかだか数年後なので、動きを追ってみましょう。
2014年1月1日⇒水曜日
2015年1月1日⇒木曜日
2016年1月1日⇒金曜日
2017年1月1日⇒日曜日(2016年はうるう年で、2月29日があるので)
2018年1月1日⇒月曜日
2019年1月1日⇒火曜日
2020年1月1日⇒水曜日
2021年1月1日⇒金曜日(2020年はうるう年で、2月29日があるので)
というわけで、2020年12月31日大晦日(おおみそか)は、一日戻って木曜日が正解。
Q3 ⇒問題
仕事算、鶴亀算の考え方について、流れの中で理解することを狙いとした出題です。
まず右手で55回なので、一回あたりは55分の1の仕事量…
といわれても、なかなかピンッとはきませんよね。
仕事算は全体を1として考えにくい場合は、
最小公倍数から全体の個数を設定すると考えやすくなる場合があります。
というわけで、55と70の最小公倍数を探ってみます。
55=5×11
70=5×2×7なので、
最小公倍数は5×11×2×7で求められそうです。
計算すると770と出てきます。
ですから、コモリンがつかむべき『つぶ』は、全部で770個あったと考えてみましょう。
すると、右手は一回で770÷55=14個、
左手は一回で770÷70=11個
の『つぶ』をつかむことができるとわかります。
さて、問1。左手の方がつかめる数が少ないので、こちらに合わせてみますね。
もしいま仮に、64回全て左手でつかんだとしたら…
64×11=704個
あれれ…770個には全然足りません。
770-704=66個分のズレが生じています。
そこで、一回だけ、左手がした仕事を右手にさせてみます。
つまり左手を63回、右手を1回としてみます。
すると11個取れなくなるけれど、14個新たに取れるわけですから、
トータルで3個『つぶ』を多く取ることができます。
ここから、左手を一回分右手にかえると、3個多く取れることがわかったわけですから、
66個のズレを解消するには…
66÷3=22回分、左手がした分を右手にかえればいいことがわかります。
というわけで、22回が正解。ちなみにこのとき、左手は42回となります。
問2について。全体770個の『つぶ』を、右手一回あたり14個と左手一回あたり11個で、
合計一回あたり25個でつかみます。
ということで、この作業にかかる回数は
770÷25=30.8回
ただし、回数は整数値で答えなければならないので、31回が正解。
Q4 ⇒問題
条件の絞り込みを考えつつ、迷路問題や一部の証明問題など、解答から問題へと戻る方が容易になる場合があることを知ることに狙いをおいた出題です。
昔ながらのマッチ棒問題でも、類似したものはいくつもあることと思います。
爪楊枝やペンなど、なんでもよいのですが、いろいろと手を動かして試行錯誤してみるのも大事。
ただ、ここでは条件の絞り込みから解答を予測して考えてみます。
条件は小さな5つの正方形であり、余分な図形や、余りの辺がありません。
そこで辺の総数をカウントしてみると…20本です。
ということは、小さな正方形が5つできるわけですから、
「各正方形の共有する辺がない」ことがわかります。ここがPOINT。
例えば次の2つの正方形について、辺の総数は7本となっております。
これは、共有辺が1つあるために、総数が8本から1本減っているわけですね。
![]()
共有辺がなければ、20本の辺で5つの正方形を作ることができます。
では、問題の図形から、辺を3つ動かすだけで、共有辺のない正方形を5つ作るとなると…
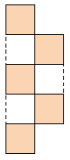
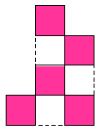
このどちらかになりますね。
逆に、このどちらかであれば、3本の辺を移動するだけで問題の図形に戻れます。
というわけで、上記のどちらでも正解となります。
※画面右上の A をクリックすることで、
文字の大きさがかわります。

 スカイシート
スカイシート